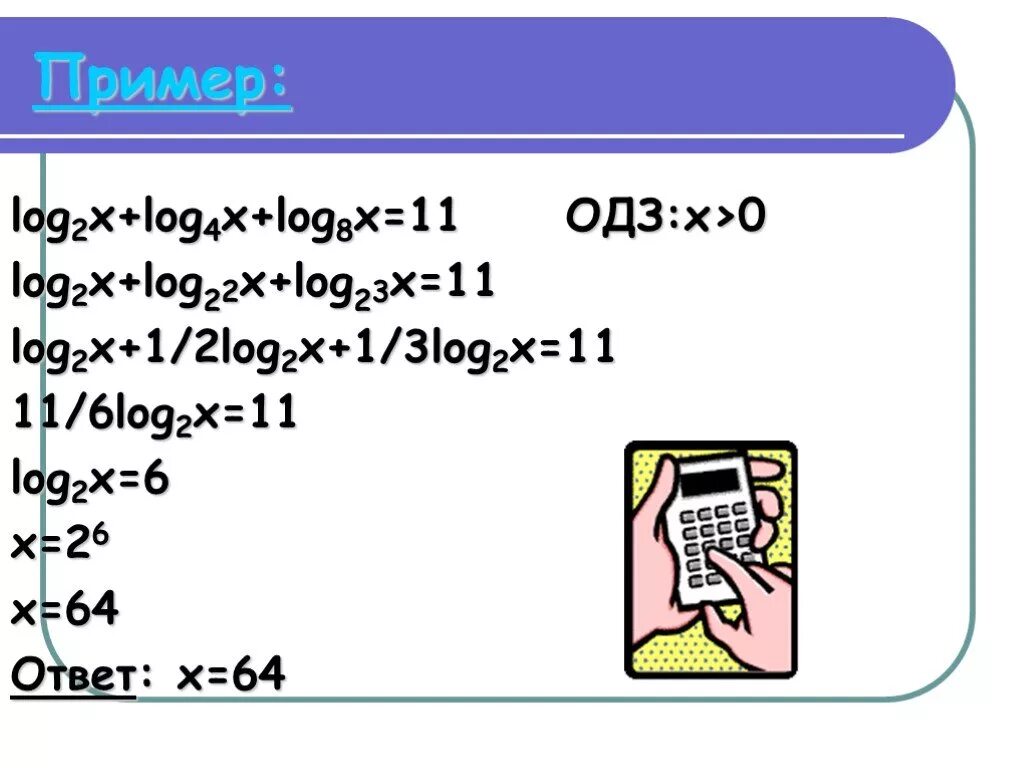
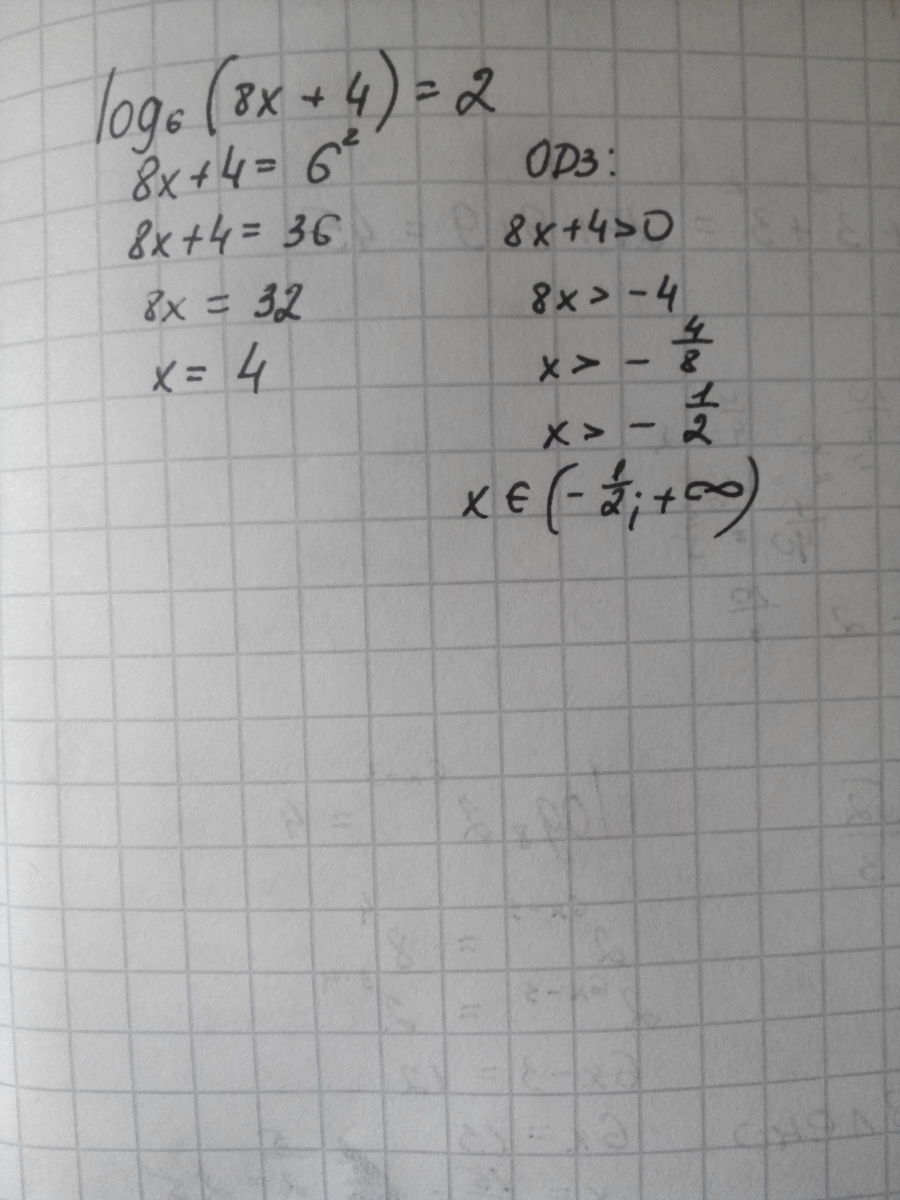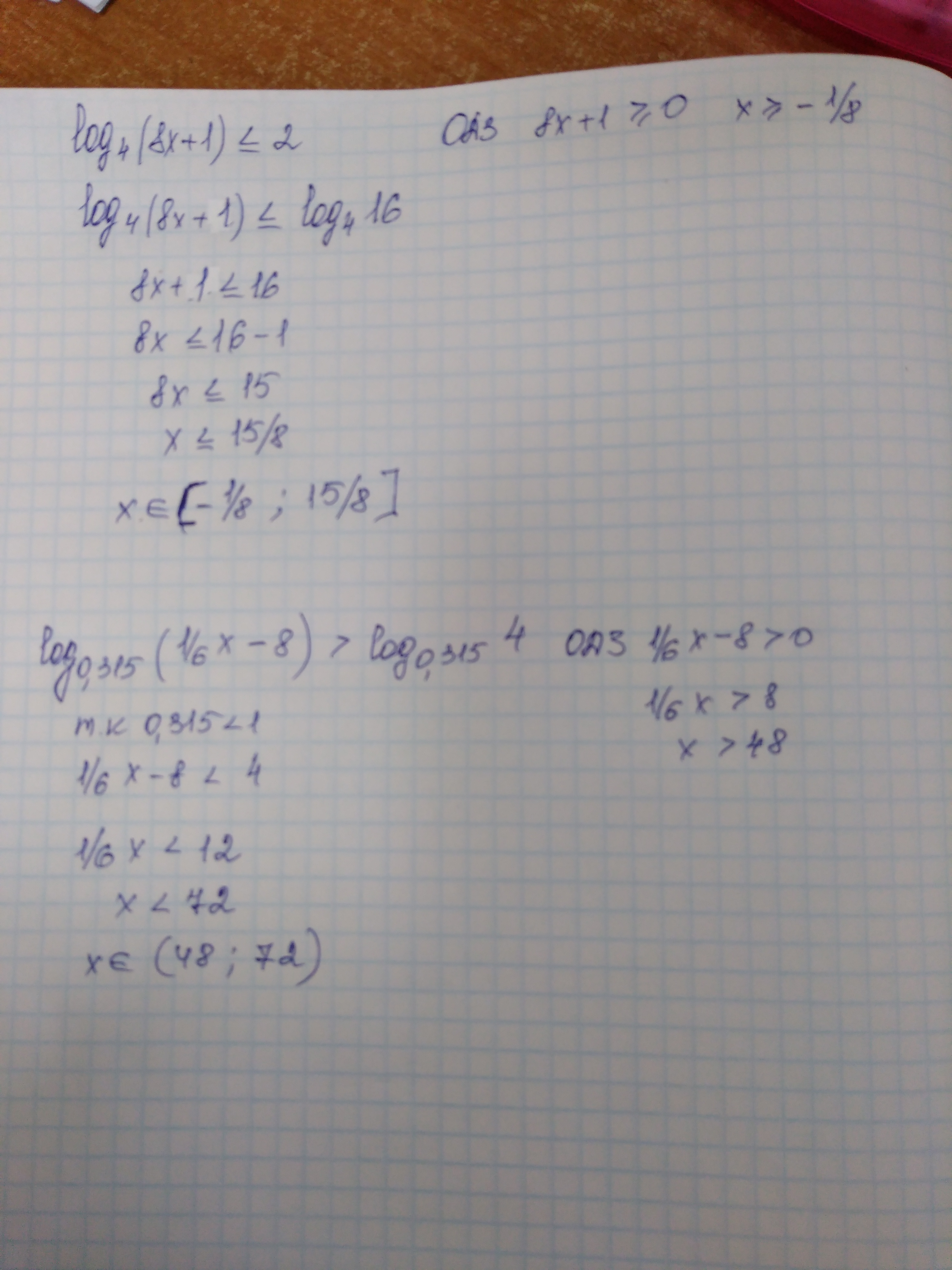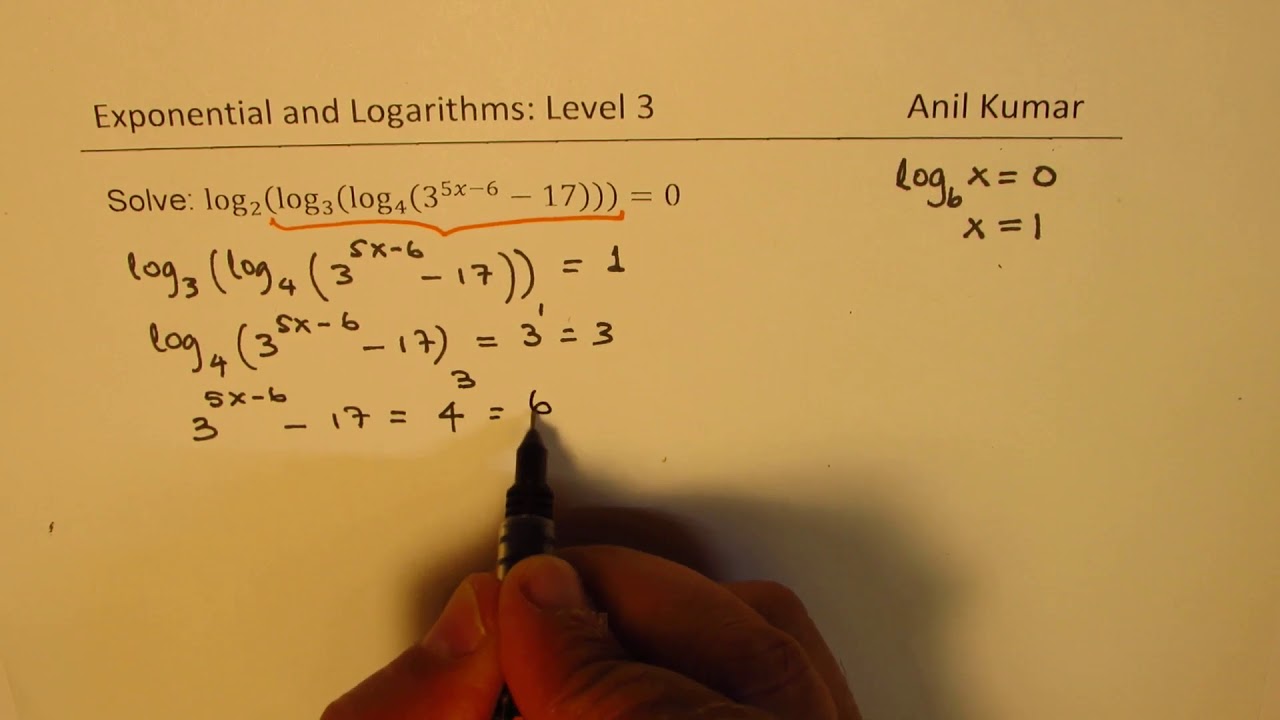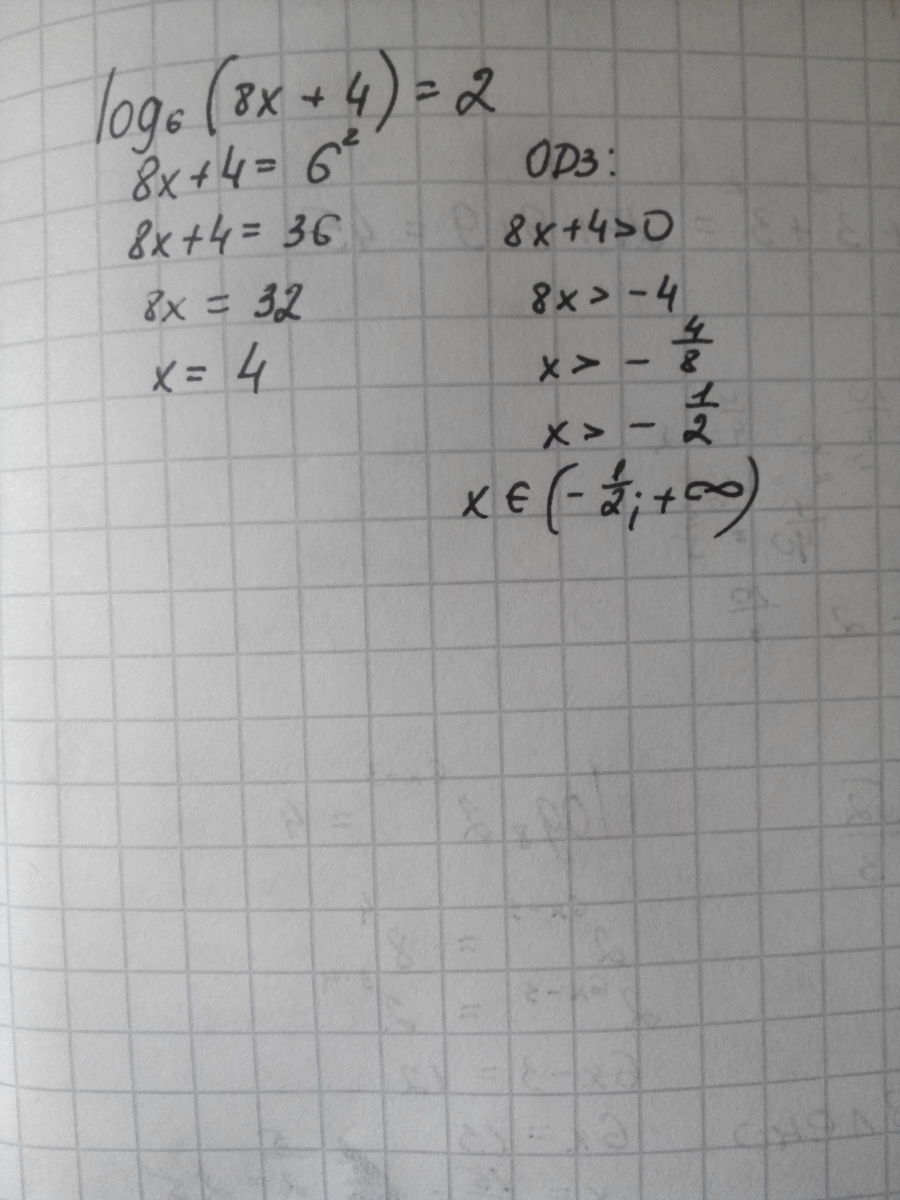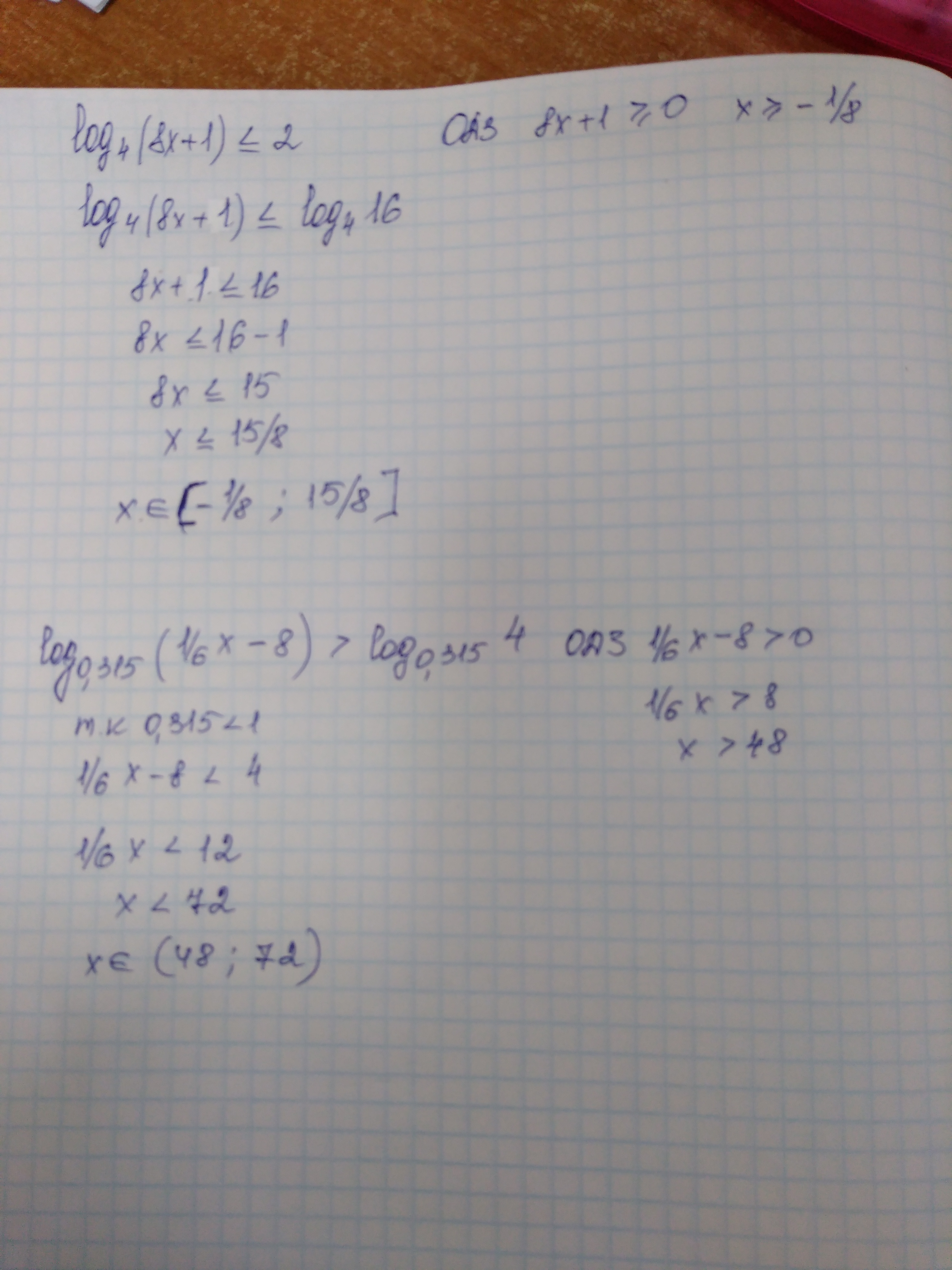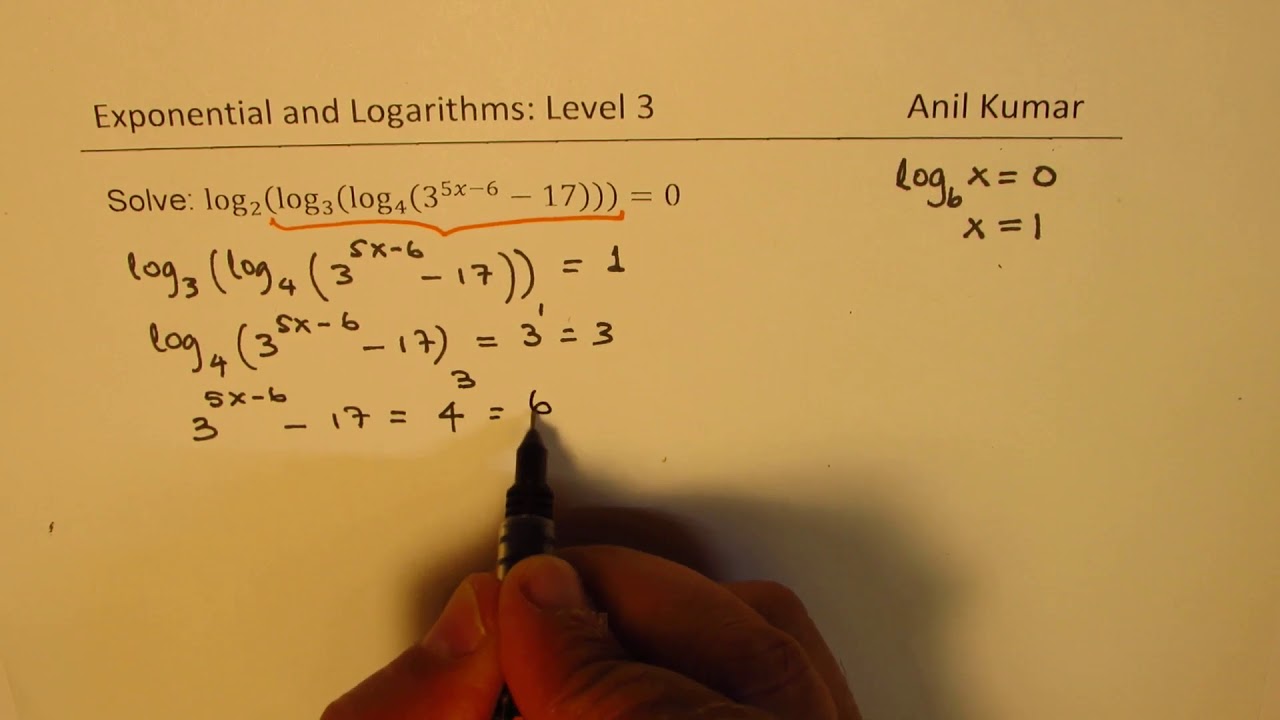Log4x>1. X2log243 -x-3 >log3 x2+ 6х 9. Log 2 3 5x-6-x 2. Log2. 4-x log2 6+2x.
Log4x>1. X2log243 -x-3 >log3 x2+ 6х 9. Log 2 3 5x-6-x 2. Log2. 4-x log2 6+2x.
|
 2 log 2x 6 4. Log2(x-1)=1-log2x. -0,5у(4-2у2)(у2+3). 6 2+лог 6 8. Log 1/2 x.
2 log 2x 6 4. Log2(x-1)=1-log2x. -0,5у(4-2у2)(у2+3). 6 2+лог 6 8. Log 1/2 x.
|
 2 (x 2 +4x )=−1 ответ. Log2 (x − 1) − log2 (x + 1) + log x+1 x−1 2 >. 4. Log 2 1/6 x>4. Решите неравенство log4(6x-8)>2.
2 (x 2 +4x )=−1 ответ. Log2 (x − 1) − log2 (x + 1) + log x+1 x−1 2 >. 4. Log 2 1/6 x>4. Решите неравенство log4(6x-8)>2.
|
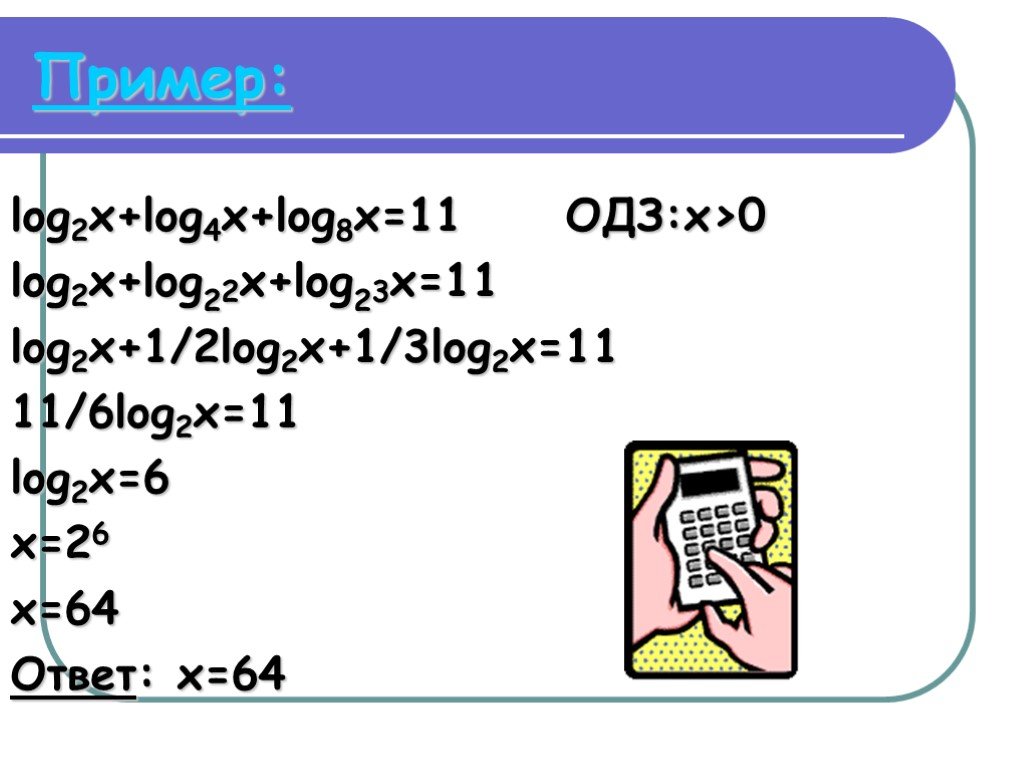
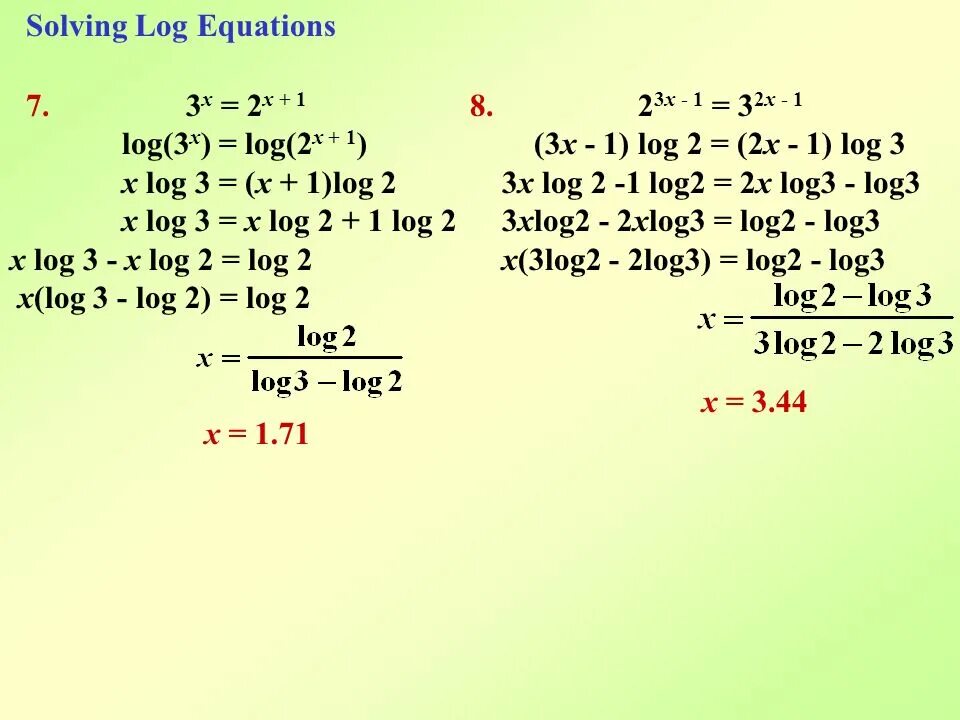 Log2x+6log4x 8. Log2 2 3 log2 12 log12 2 log2 144 log3 2. Log6 2x-1 log6 3x+4. (log (9) 2- log (9) 4)* log(2) 9. Log1 2 3 5х 3.
Log2x+6log4x 8. Log2 2 3 log2 12 log12 2 log2 144 log3 2. Log6 2x-1 log6 3x+4. (log (9) 2- log (9) 4)* log(2) 9. Log1 2 3 5х 3.
|
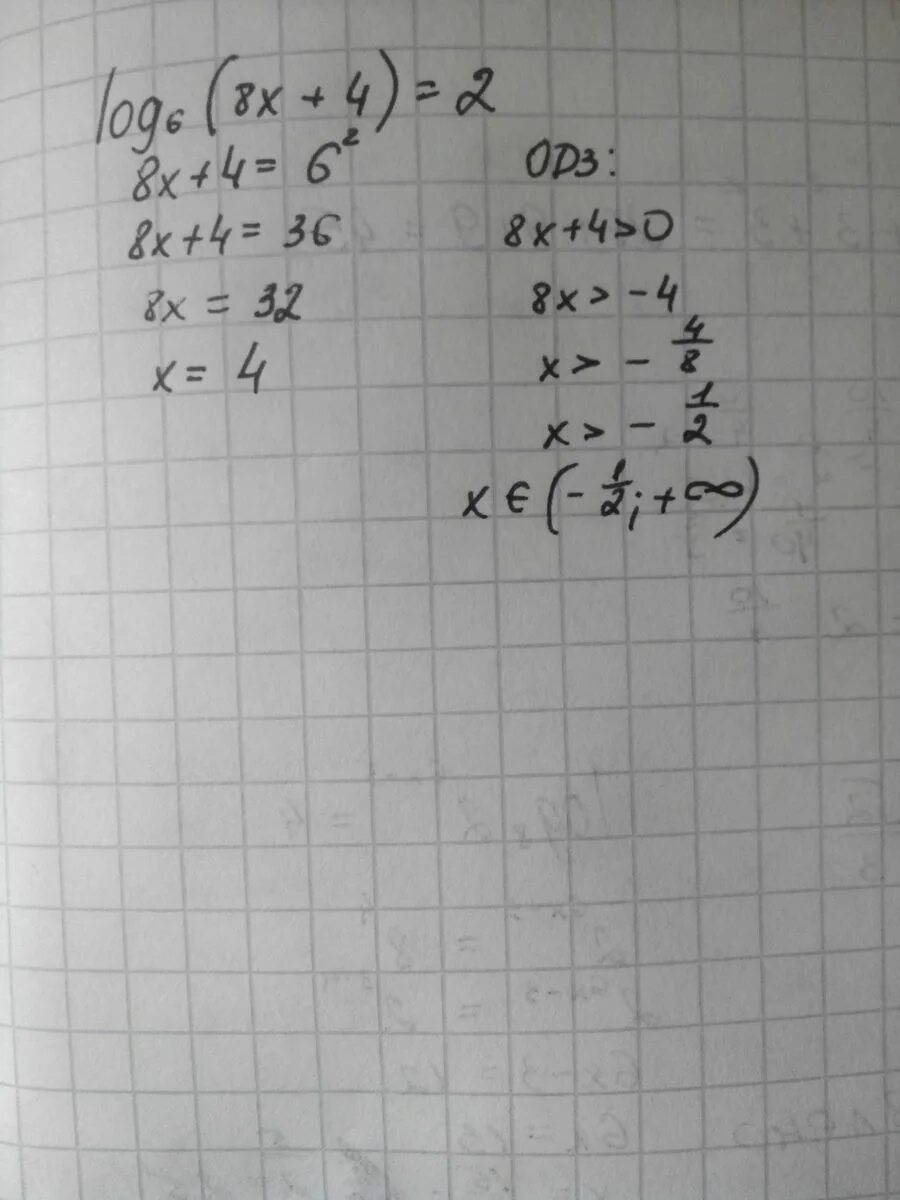 2 log 2x 6 4. Логарифмические уравнения log2 (x+1) = 3-log2 4. 2 log 2x 6 4. 2 log 2x 6 4. Log4x=2.
2 log 2x 6 4. Логарифмические уравнения log2 (x+1) = 3-log2 4. 2 log 2x 6 4. 2 log 2x 6 4. Log4x=2.
|
 Log2(x+2) уравнение. Log4 8. Log1/4 (x^2+6x)=-2. X 2 log243 4-x log3 x 2-8x+16. 2 log 2x 6 4.
Log2(x+2) уравнение. Log4 8. Log1/4 (x^2+6x)=-2. X 2 log243 4-x log3 x 2-8x+16. 2 log 2x 6 4.
|
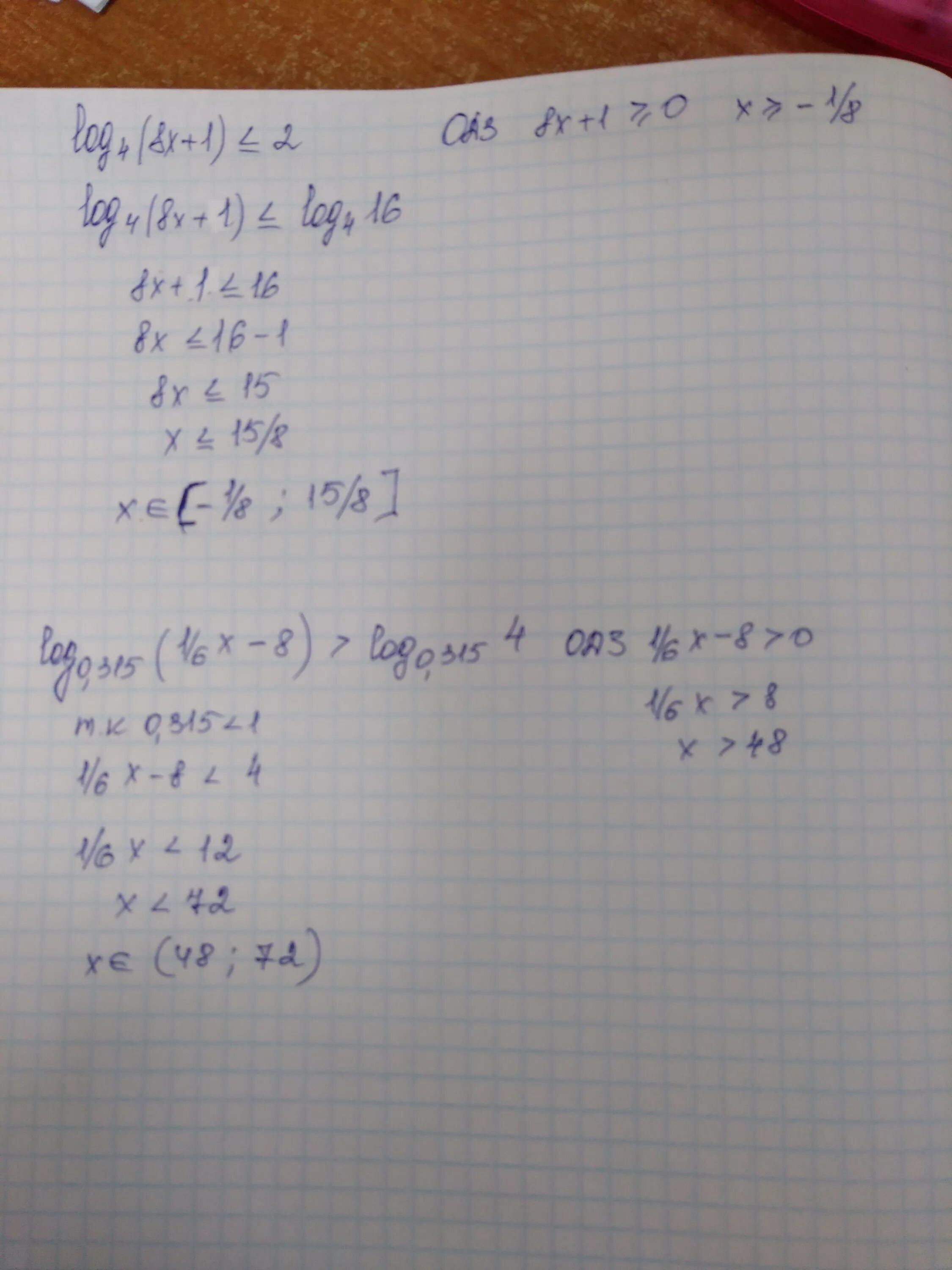 2 log 2x 6 4. Log0,2(x–2) (4x–8)(|x|–5) ≥ 0 математика 10. Логарифмические уравнения log2/3 + log3. Log2x x-4 logx-1 6-x 0. Log4x>1.
2 log 2x 6 4. Log0,2(x–2) (4x–8)(|x|–5) ≥ 0 математика 10. Логарифмические уравнения log2/3 + log3. Log2x x-4 logx-1 6-x 0. Log4x>1.
|
 Корень уравнения с логарифмами. Log4 x-6 2log4x. Log2x. Решите неравенство: log2(𝑥 − 8) < 1. 2 log 2x 6 4.
Корень уравнения с логарифмами. Log4 x-6 2log4x. Log2x. Решите неравенство: log2(𝑥 − 8) < 1. 2 log 2x 6 4.
|
 Системы логарифмических уравнений. Лог2 1. Лог 8 2 8х-4 4. 10 log10 2. -2log4 (6x+1)=1.
Системы логарифмических уравнений. Лог2 1. Лог 8 2 8х-4 4. 10 log10 2. -2log4 (6x+1)=1.
|
 Log12(log4(log3(x+1)=0. Решить уравнение log. Log5(4+х)=2. 2 log 2x 6 4. Log в квадрате 2 2-x.
Log12(log4(log3(x+1)=0. Решить уравнение log. Log5(4+х)=2. 2 log 2x 6 4. Log в квадрате 2 2-x.
|
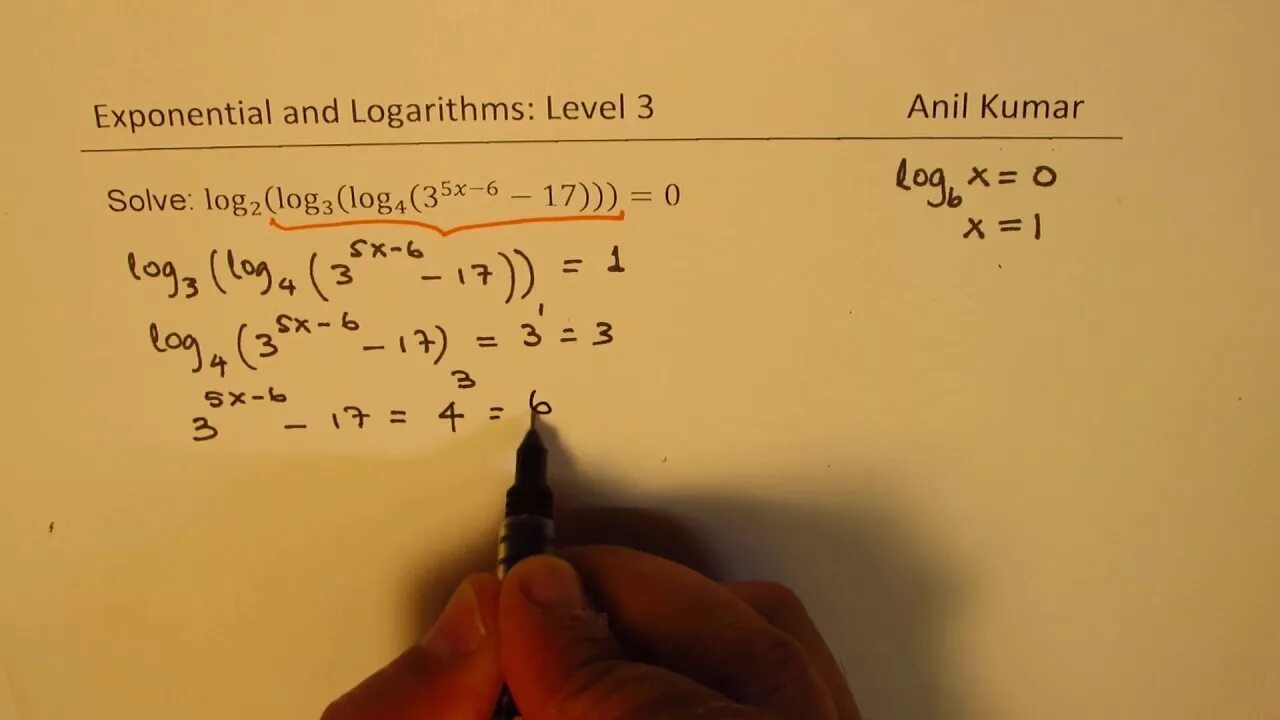 Log 4 х+2 = 2. Решение логарифмических уравнений. Log6 8+x 2. Log4 x-6 2log4x. Лог 4.
Log 4 х+2 = 2. Решение логарифмических уравнений. Log6 8+x 2. Log4 x-6 2log4x. Лог 4.
|
 Log4x. Log 2 1/6 x>4. Log2x/log2x-6. 2 log 2x 6 4. Лог 1/4 (2х+1)=-1.
Log4x. Log 2 1/6 x>4. Log2x/log2x-6. 2 log 2x 6 4. Лог 1/4 (2х+1)=-1.
|
 Log4 (2x-1)=1. 2 (2x-4) = -2. Log10t>log3t. 2 log 2x 6 4. 2log2 (2x-2) <= x.
Log4 (2x-1)=1. 2 (2x-4) = -2. Log10t>log3t. 2 log 2x 6 4. 2log2 (2x-2) <= x.
|
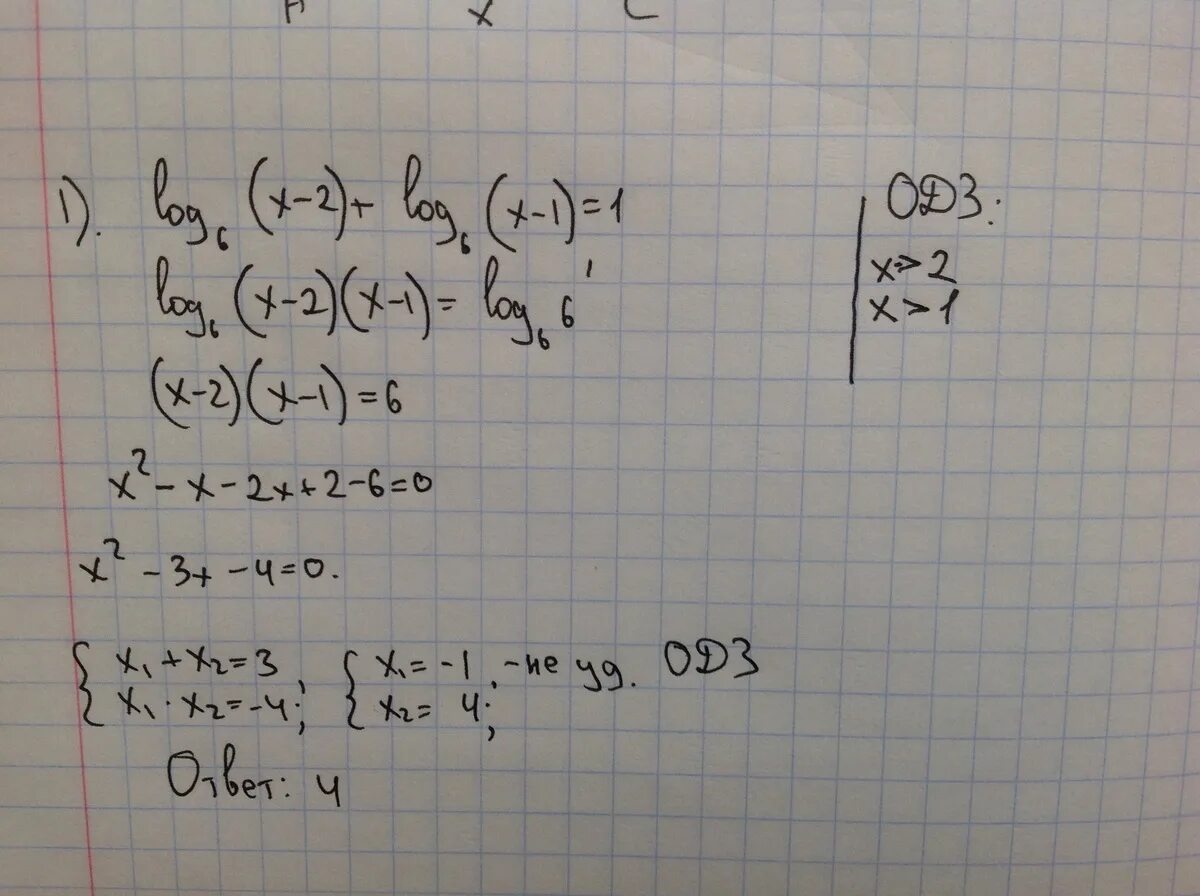 Введение новой переменной логарифмических уравнений. 2 log 2x 6 4. Log3(x2-5x+4)-log3(x-4)=2. Log2x=3. Log4(x^2+4x-5).
Введение новой переменной логарифмических уравнений. 2 log 2x 6 4. Log3(x2-5x+4)-log3(x-4)=2. Log2x=3. Log4(x^2+4x-5).
|
 Лог 0. 2 log 2x 6 4. Log 2 2x log 0. Метод введения новой переменной логарифмические уравнения. 2x-1/6+x-1/2=1.
Лог 0. 2 log 2x 6 4. Log 2 2x log 0. Метод введения новой переменной логарифмические уравнения. 2x-1/6+x-1/2=1.
|
 : log_0,2 (2x-6)>log_0,2 (x^2+3). Log2 2. Log 1/2 x. Log3 log4 log2/3 x-3 0. 2 log 2x 6 4.
: log_0,2 (2x-6)>log_0,2 (x^2+3). Log2 2. Log 1/2 x. Log3 log4 log2/3 x-3 0. 2 log 2x 6 4.
|
 4log5 x-2 +1/log5 2 x-2 +log5 x-2. 2 log 2x 6 4. Log2 (log6 x) = 1. 2 log 2x 6 4. Log2x больше 3.
4log5 x-2 +1/log5 2 x-2 +log5 x-2. 2 log 2x 6 4. Log2 (log6 x) = 1. 2 log 2x 6 4. Log2x больше 3.
|
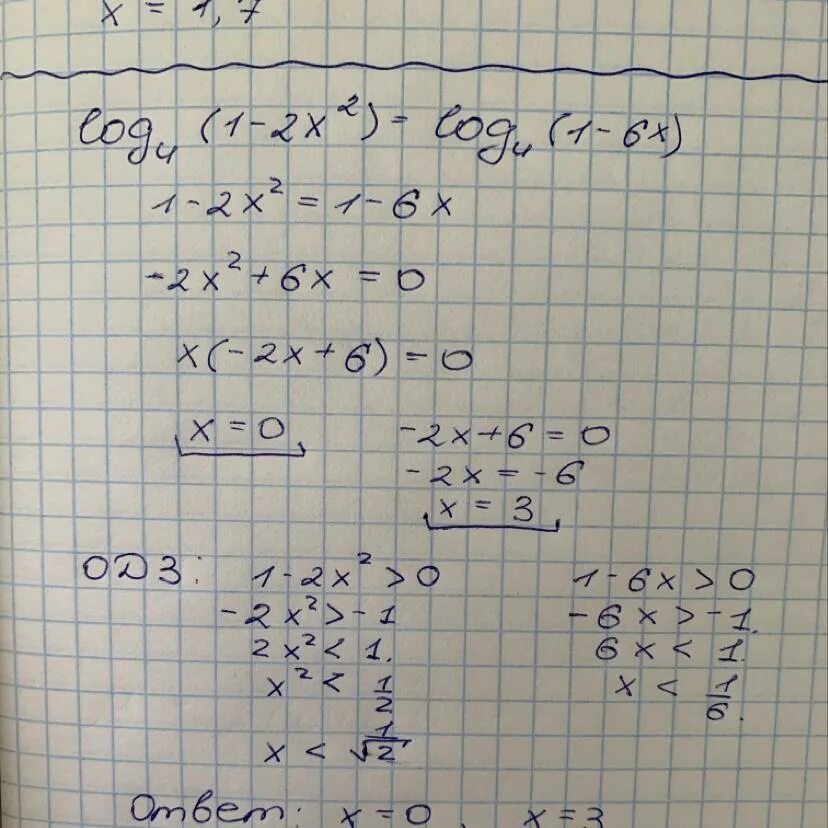 Log ( 3 ) 2 2 0,5 х + х −. Лог 2/2 (4-х)+лог 1/4 (8/4-х)=2 в степени лог4(9). 5. 2 log 2x 6 4. Х 2 log243 ( - х - 3) > log3 (х 2 + 6х + 9).
Log ( 3 ) 2 2 0,5 х + х −. Лог 2/2 (4-х)+лог 1/4 (8/4-х)=2 в степени лог4(9). 5. 2 log 2x 6 4. Х 2 log243 ( - х - 3) > log3 (х 2 + 6х + 9).
|
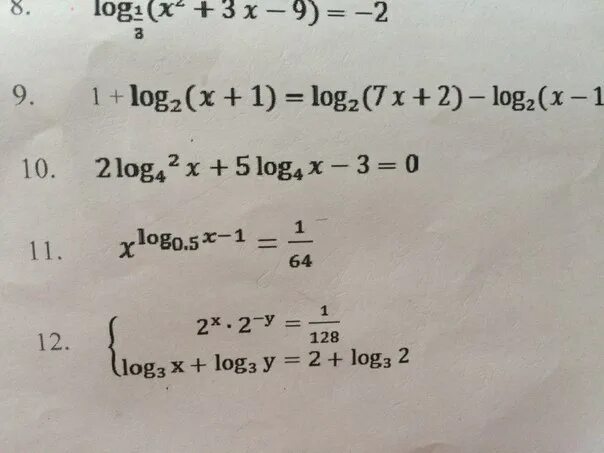 2 log 2x 6 4. Решение log уравнений. Log4x= -2 решение. 2 log 2x 6 4. Log4 (2log 3 (x)=0.
2 log 2x 6 4. Решение log уравнений. Log4x= -2 решение. 2 log 2x 6 4. Log4 (2log 3 (x)=0.
|
 2 log 2x 6 4. Log2(6-x)=log216 ответ. Log2 x > 4 одз. Log 0. 2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3.
2 log 2x 6 4. Log2(6-x)=log216 ответ. Log2 x > 4 одз. Log 0. 2log_12〖(х+6/(х-5)〗)=log_12〖(3/(х-2)〗 - 2/(х-3))+3.
|